सर्वप्रथम हम तरंगाग्र को हम परिभाषित करेंगे | जब हम किसी शांत जल के तालाब में एक छोटा पत्थर फेंकते है तब प्रतिघात बिंदु से चारों ओर तरंगें फैलती हैं पृष्ठ का प्रत्येक बिंदु समय के साथ दोलन करना प्रारंभ कर देता है | किसी एक क्षण पर पृष्ठ का फ़ोटोग्राफ़ उन वृताकार वलयों को दर्शाएगा जिनके ऊपर विक्षोभ अधिकतम हैं | स्पष्टत : इस प्रकार के वृत्त के सभी बिंदु समान कला में दोलन करते हैं क्योंकि वे स्त्रोत से समान दुरी पर हैं | समान कला में दोलन करते ऐसे सभी बिंदुओं का बिंदु पथ तरंगाग्र कहलाता है |
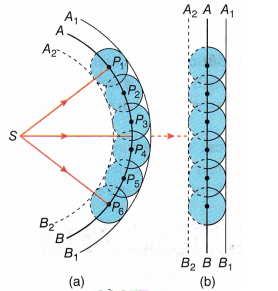
अत : एक तरंगाग्र को एक समान कला के पृष्ठ के रूप में परिभाषित किया जाता है | जिस गति के साथ तरंगाग्र स्रोत से बहार की ओर बढ़ता है , वह तरंग की चाल कहलाती है | तरंग की उर्जा तरंगाग्र के लंबवत चलती है | यदि एक बिंदु –स्रोत प्रत्येक दिशा में एक समान तरंगे उत्सर्जित करता है तो उन बिंदुओं का बिंदुपथ , जिनका आयाम समान है और जो एक समान कला में कंपन करते है , गोला होता है तथा हमें चित्र की भाँती एक गोलीय तरंग प्राप्त होती है | स्रोत से बहुत अधिक दूरी पर , गोले का एक छोटा भाग समतल माना जा सकता है और हमें एक समतल तरंग प्राप्त होता है | अब यदि हमें t =0 पर किसी तरंगाग्र की आकृति ज्ञात है तो हाइगेंस के सिद्धांत द्वारा हम किसी बाद के समय T पर तरंगाग्र की आकृति ज्ञात कर सकते हैं |अत: हाइगेंस का सिद्धांत वास्तव में एक ज्यामितीय रचना है जो किसी समय यदि तरंगाग्र की आकृति ज्ञात कर सकते हैं | आइए , एक अपसरित तरंग के बारे में विचार करें और मान लीजिए f-(1)f-2, t = 0 समय पर एक गोलीय तरंगाग्र के एक भाग को प्रदर्शित करता है| अब हाइगेंस के सिद्धांत के अनुसार , तरंगाग्र का प्रत्येक बिंदु एक द्वितीयक विक्षोप का स्रोत है और इन बिंदुओं से होने वाली तरंगिकाए तरंग की गति से सभी दिशाओं में फैलती हैं | तरंगाग्र से निर्गमन होने वाली इन तरंगिकाओं को प्राय : द्वितीयक तरंगिकाओं के नाम से जाना जाता है और यदि हम इन सभी गोलों पर एक उभयनिष्ठ स्पर्शक पृष्ठ खीचें तो हमें किसी बाद के समय पर तरंग की नयी स्थिति प्राप्त हो जाती है | अत : यदि हम t = t समय पर तरंगाग्र की आकृति ज्ञात करना चाहते हैं तो हम गोलीय तरंगाग्र के प्रत्येक बिंदु से UT त्रिज्या के गोले खींचेंगे , जहाँ पर U माध्यम में तरंग की चाल को निरुपित करता है | यदि हम इन सभी गोलों पर एक उभयनिष्ठ स्पर्श रेखा खींचे , तो हमें t =T समय पर तरंगाग्र की नयी स्थति प्राप्त होगी | उपरोक्त मॉडल में एक दोष है | हमें एक पश्य तरंग भी प्राप्त होती है | हाइगेंस ने तर्क प्रस्तुत किया कि आगे की दिशा में द्वितीयक तरंगिकाओं का आयाम अधिकतम होता है तथा पीछे की दिशा में यह शून्य होता है | इस तदर्थ कल्पना से हाइगेंस पश्य तरंगों की अनुपस्थित का औचित्य वास्तव में एक अधिक परिशुद्ध तरंग सिद्धांत द्वारा बताया जा सकता है | इस विधि द्वारा हम हाइगेंस के सिद्धांत का उपयोग किसी माध्यम में संचरित होने वाली समतल तरंग के तरंगाग्र की आकृति ज्ञात करने के लिए कर सकते हैं |
